Da jeg begyndte at tabe mig stod valget med to modeller. I model nummer 1, skal jeg indtage en mængde kcal passende sig for en fyr der vejede det jeg gerne ville veje. Så hvis jeg gerne ville veje 90 kg skulle jeg bare gå ind på Go Motion og regne det ud. Det bliver for en mand i min alder 2673,2 kcal/dag.
Jeg valgte model nummer 2, som jeg har skrevet om tidligere. Kort fortalt bestemmer jeg mig for, hvor meget jeg vil tabe mig, regner tallet om til den mængde kcal jeg skal være i underskud med over den valgte periode, vælger den periodelængde, som jeg vil tabe mig over, og dividerer de to tal med hinanden. Så ved jeg, hvor mange kcal jeg skal være i underskud med pr. dag.
Her vil jeg vise, at model nummer 2 leder til det ønskede vægttab, mens model nummer 1 ikke gør. Der kan sikkert siges en masse andet om de to modeller, og jeg tror i det hele taget at model nummer 2 er bedst, men lad os komme i gang med den matematiske modellering.
Vægtudvikling med metode nummer 1
Præmissen er altså, at jeg indtager det antal kcal/dag, E_f=19.68*m_f+902 kcal, som en person med min ønskede vægt skal indtage for at holde netop den vægt. Da jeg vejer et antal kg - vi kalder dette antal for m - vil jeg hver dag forbrænde E=19.68*m+902 kcal ifølge WHO. Mit daglige energiunderskud er da E_f - E. Det fedt jeg har på kroppen vejer nogle kg. Disse kan omsættes til energi, så det energiunderskud jeg opnår udmønter sig til syvende og sidst i, at jeg taber nogle kg, svarende til et vist antal kcal. Dette energiunderskud kalder jeg dE.
Jeg har brugt den notation, man normalt bruger, når man skal løse differentialligninger, så det lille d foran E'et ovenfor betyder at det er en rimelig lille ændring per dag vi snakker om. Faktisk behøver enheden ikke at være dage - det kan sagtens bare være sekunder, millisekunder eller nanosekunder. Når man skriver alt dette op som en matematisk ligning ser det således ud:
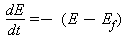 Vi kan kalde den energiligningen. Det lille dt fortæller os, at vi snakker ændringen i opsparet energi i form af fedt pr. tidsenhed. Men hvad sker der lige med minustegnene på højresiden? Hvis du kigger ovenfor kan du se, at de to E'er på højresiden har byttet plads. Det kan man gøre, hvis man rykker et minustegn uden for parentesen. Hvis du ganger minustegnet ind og bytter om på de to igen, får du samme udtryk som i paragraffen ovenover.
Vi kan kalde den energiligningen. Det lille dt fortæller os, at vi snakker ændringen i opsparet energi i form af fedt pr. tidsenhed. Men hvad sker der lige med minustegnene på højresiden? Hvis du kigger ovenfor kan du se, at de to E'er på højresiden har byttet plads. Det kan man gøre, hvis man rykker et minustegn uden for parentesen. Hvis du ganger minustegnet ind og bytter om på de to igen, får du samme udtryk som i paragraffen ovenover.Venstre side i energiligningen
Det E der står på venstresiden kan vi udtrykke på en anden måde. Vi ved nemlig at 1 g fedt svarer til energien 7,4 kcal. Så må 1 kg, 1000 g, svare til 7400 kcal. Sagt på formelprog: E = k*m, hvor k er en konstant med værdien 7400 kcal/kg. Når man i matematik beskæftiger sig med differentialregning, bruger man ofte differentialet af en funktion. Differentialet fortæller os hvad der sker med en funktions enkelte bestanddele, når funktionen ændres en lille bitte smule. Et differentiale er altså et mål for meget små ændringer. Tager vi nu differentialet af vores E - det symboliserer vi ved at skrive det der d foran - så ved vi, at det der ændrer sig er vægten, m. k var jo en konstant, og derfor kan det ikke ændres. Så dE = k*dm.
Højresiden i energiligningen
På højresiden kan vi bruge WHOs formler:
E - E_f = 19.68*m + 902 -(19.68*m_f + 902) kcal
E - E_f = 19.68*m - 19.68*m_f kcal =19.68*(m - m_f) kcal
E - E_f = 19.68*m - 19.68*m_f kcal =19.68*(m - m_f) kcal
Tallet 19.68 kcal/kg er kun for mænd i alderen 31-60 år, og der gælder andre regler for andre aldersklasser. Så jeg vil i det følgende bare kalde dette tal for c, for så kan vi ændre på det, hvis vi får lyst. Det vil sige, at vores ligning nu hedder:
Eller for nu at bruge omskrivningen dE=k*dm:
Her har jeg divideret med k på begge sider af lighedstegnet. Det må man gerne! Hvis ellers k ikke har værdien 0. Den ligning vi er kommet frem til, er en differentialligning. Den kan man løse, hvis man ellers kan matematik. Her følger udregningerne for de interesserede. Hvis du ikke er interesseret, skal du bare scrolle ned til jeg siger STOP.
Først kan man konstatere, at
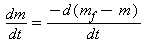
Her har jeg divideret med k på begge sider af lighedstegnet. Det må man gerne! Hvis ellers k ikke har værdien 0. Den ligning vi er kommet frem til, er en differentialligning. Den kan man løse, hvis man ellers kan matematik. Her følger udregningerne for de interesserede. Hvis du ikke er interesseret, skal du bare scrolle ned til jeg siger STOP.
Først kan man konstatere, at
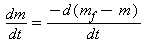
Det er fordi m_f er en konstant og der er et minus foran m. Så differentialligningen kunne omskrives til:
Nu kan jeg dividere med (m_f - m) på begge sider. Samtidig kan jeg gange med -1 på begge sider. Så får jeg
Det der ln står for den naturlige logaritme. Differentierer man den ovenstående logaritmefunktion får man faktisk venstresiden fra før divideret med (m_f - m). Differentialligningen er nem at løse, det bliver bare:
Her kommer K'et ind som en integrationskonstant. Det er fordi, når vi differentierer med hensyn til t, så forsvinder K'et alligevel. Så det er den mest generelle løsning.
Den naturlige logaritme har en invers som hedder eksponentialfunktionen. Begge ting og deres indbyrdes relationer kan du læse om i matematikbøger fra gymnasiet. Tager vi eksponentialfunktionen på begge sider får vi:
Her er K'et fanget i konstanten C. Vi har endnu ikke bestemt disse konstanter, men det kommer. I hvert fald for C's vedkommende. Bytter vi lidt rundt får vi:
Nu vil vi gerne bestemme C. Sætter vi t=0 giver eksponentialfunktion 1. Men hvorfor skulle vi dog finde på at sætte t=0? Jo, jeg skal jo begynde min slankning på et eller andet tidspunkt, og den dag jeg begynder, er dag 0. Men hvis eksponentitalfunktionen giver 1, så står der jo, at
Her er m_f min ønskede vægt og m_s = m(0) min startvægt. Men hov, mit ønskede vægttab er jo
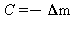
Nu kan jeg dividere med (m_f - m) på begge sider. Samtidig kan jeg gange med -1 på begge sider. Så får jeg
Det der ln står for den naturlige logaritme. Differentierer man den ovenstående logaritmefunktion får man faktisk venstresiden fra før divideret med (m_f - m). Differentialligningen er nem at løse, det bliver bare:
Her kommer K'et ind som en integrationskonstant. Det er fordi, når vi differentierer med hensyn til t, så forsvinder K'et alligevel. Så det er den mest generelle løsning.
Den naturlige logaritme har en invers som hedder eksponentialfunktionen. Begge ting og deres indbyrdes relationer kan du læse om i matematikbøger fra gymnasiet. Tager vi eksponentialfunktionen på begge sider får vi:
Her er K'et fanget i konstanten C. Vi har endnu ikke bestemt disse konstanter, men det kommer. I hvert fald for C's vedkommende. Bytter vi lidt rundt får vi:
Nu vil vi gerne bestemme C. Sætter vi t=0 giver eksponentialfunktion 1. Men hvorfor skulle vi dog finde på at sætte t=0? Jo, jeg skal jo begynde min slankning på et eller andet tidspunkt, og den dag jeg begynder, er dag 0. Men hvis eksponentitalfunktionen giver 1, så står der jo, at
Her er m_f min ønskede vægt og m_s = m(0) min startvægt. Men hov, mit ønskede vægttab er jo
Så er C altså minus det ønskede vægttab:
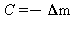
STOP!
Ligningen for mit er vægttab ud fra model 1 er altså
Jeg ønsker en vægt på m_f = 90 kg. Jeg begyndte på 135 kg. Det giver et ønsket vægttab på 45 kg. Tallet c/k fås ved at dividere c=19.68kcal/kg/dag med tallet k=7400 kcal/kg. På figuren til sidst kan du se en graf, der viser hvordan mit vægttab ifølge denne model skrider frem.
Læg mærke til, at grafen starter meget stærkt, men så flader den ud. Det er kendetegnende for netop eksponentielle funktioner, og faktisk når jeg aldrig min ønskede vægt. Det kan du se ved at kigge på formlen ovenfor. Der står jo, at min vægt altid vil være min ønskede vægt m_f plus et tal der er større end 0. Det kan da godt være, at dette tal bliver meget lille, men det vil altid være større end 0. Så min vægt vil altid være større end min ønskevægt med denne metode. Øv, altså.
Vægttab med metode nummer 2
Heldigvis er metode nummer 2 meget nemmere at regne på. Her regner jeg nemlig med et fast vægttab på k kg/dag. Hvis jeg for eksempel vil tabe mig 20 kg på 200 dage er k = 0,1 kg/dag. Jeg får altså en noget simplere differentialligning, som hedder:
Løsningen er en lineær funktion:

Ligningen for mit er vægttab ud fra model 1 er altså
Jeg ønsker en vægt på m_f = 90 kg. Jeg begyndte på 135 kg. Det giver et ønsket vægttab på 45 kg. Tallet c/k fås ved at dividere c=19.68kcal/kg/dag med tallet k=7400 kcal/kg. På figuren til sidst kan du se en graf, der viser hvordan mit vægttab ifølge denne model skrider frem.
Læg mærke til, at grafen starter meget stærkt, men så flader den ud. Det er kendetegnende for netop eksponentielle funktioner, og faktisk når jeg aldrig min ønskede vægt. Det kan du se ved at kigge på formlen ovenfor. Der står jo, at min vægt altid vil være min ønskede vægt m_f plus et tal der er større end 0. Det kan da godt være, at dette tal bliver meget lille, men det vil altid være større end 0. Så min vægt vil altid være større end min ønskevægt med denne metode. Øv, altså.
Vægttab med metode nummer 2
Heldigvis er metode nummer 2 meget nemmere at regne på. Her regner jeg nemlig med et fast vægttab på k kg/dag. Hvis jeg for eksempel vil tabe mig 20 kg på 200 dage er k = 0,1 kg/dag. Jeg får altså en noget simplere differentialligning, som hedder:
Løsningen er en lineær funktion:

Jeg har plottet de to modeller herunder. Jeg har valgt at begynde med en vægt på 135 kg og at tabe mig 0,07 kg/dag med model 2. I model 1 spiser jeg som en der vejer 90 kg gennem hele forløbet. Du kan se, at jeg med metode 2 når mit mål efter 644 dage, mens jeg med metode 1 aldrig når det. Faktisk er jeg med metode 1 ca. 8 kg bagefter, når jeg med metode 2 når målet.
 Med metode 2 kommer jeg i en periode til at spise mindre end jeg skal spise, når jeg når 90 kg. Men det hele sker gradvist, og det tror jeg er en fordel fremfor metode 1, hvor jeg med det samme nedsætter mit forbrug drastisk.
Med metode 2 kommer jeg i en periode til at spise mindre end jeg skal spise, når jeg når 90 kg. Men det hele sker gradvist, og det tror jeg er en fordel fremfor metode 1, hvor jeg med det samme nedsætter mit forbrug drastisk.
 Med metode 2 kommer jeg i en periode til at spise mindre end jeg skal spise, når jeg når 90 kg. Men det hele sker gradvist, og det tror jeg er en fordel fremfor metode 1, hvor jeg med det samme nedsætter mit forbrug drastisk.
Med metode 2 kommer jeg i en periode til at spise mindre end jeg skal spise, når jeg når 90 kg. Men det hele sker gradvist, og det tror jeg er en fordel fremfor metode 1, hvor jeg med det samme nedsætter mit forbrug drastisk.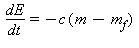
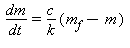
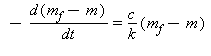

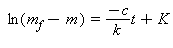
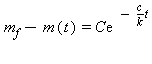

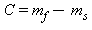
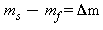
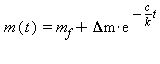


1 comment:
Jeg er målløs ...
Post a Comment